HashMap과 Red-Black Tree
HashMap
HashMap은 Map이라는 인터페이스를 구현한 구현체 중 하나이다.
hash code
hash code는 객체를 식별하는 하나의 정수값이다.
hashcode() 메소드는 객체의 주소가 담긴 객체 고유의 해시코드를 반환한다.
HashMap의 데이터 관리 방식
HashMap에서는 데이터를 저장할 때에, 버킷으로 불리는 배열을 가지고 데이터를 저장한다. 아래 table이 그 배열이다.

이 table 배열은 hash값, 키, 데이터, 다음 node 를 필드로 가진다.
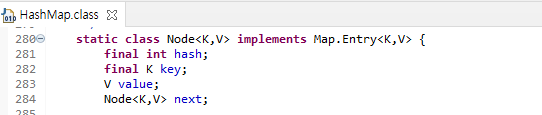
Map에 저장하는 각 데이터는 고유한 키값으로 구분할 수 있다.
HashMap에서는 이 키값에 대해, hash code를 추출하고, 그 hash code를 배열의 크기로 나눈 나머지를 내부 배열의 인덱스로 설정해 저장하고, 값을 조회한다.
HashMap은 인덱스를 통해 데이터에 접근하기 때문에, O(1)의 시간 복잡도를 갖는다.
배열 크기 조정을 통한 HashMap의 충돌 관리
hash code의 기준을 잘 설정한다면 각 키에 대한 hash code의 중복, 즉 충돌이 발생하지 않겠지만, 완전히 보장할 수는 없다.
그래서 HashMap은 버킷(배열)의 75%를 초과하여 채워지면, 버킷의 사이즈를 2배씩 늘려 키 값 간 충돌을 방지한다.
LinkedList와 Red-Black Tree를 통한 HashMap의 충돌 관리
배열 크기를 조정하는 것 뿐으로는 충돌을 관리하기 어렵다.
만약, 충돌이 발생하여 하나의 인덱스에 여러 데이터가 저장되어야하는 상황이 발생한다면, 같은 인덱스를 가지는 데이터를 LinkedList로 연결하거나 Red-Black Tree로 연결한다.
LinkedList를 사용한 Seperate Chaining 방식
LinkedList로 같은 인덱스를 가지는 각 노드를 연결한 방식을 Seperate Chaining 방식이라고 부른다.
LinkedList를 사용하기 때문에, 데이터를 조회할 때, O(n)의 시간 복잡도를 가진다.

Red-Black Tree 방식
충돌횟수가 일정 수치( TREEIFY_THRESHOLD -1 )를 초과하면, O(n)으로 데이터를 탐색하는 것이 비효율적이다. 이때, Red-Black Tree 방식을 사용한다.
Balanced Tree 구조이기 때문에, 데이터를 조회할 때, O(log n)의 시간 복잡도를 가진다. 따라서, 탐색 속도가 LinkedList를 사용한 방식보다 빠르다.
왜 다른 Balanced Search Tree - AVL Tree가 아닌 Red-Black Tree를 사용한걸까?
Red-Black Tree와 같은 Balanced Search Tree 인 AVL Tree도 사용할 수 있을 텐데, 왜 HashMap은 Red-Black Tree를 사용한 걸까? 게다가, AVL Tree가 더 엄격하게 균형있는 트리로 관리하기 때문에, 탐색 속도가 빠르다.
- HashMap은 삽입, 삭제가 자주 일어난다.
- AVL Tree는 더 엄격한 균형의 트리인 만큼, 삽입과 삭제에 대해 Red-Black Tree보다 느리다.
- Red-Black Tree는 rebalance 시에, color flip과 rotate로 비교적 빠르게 삽입과 삭제를 수행할 수 있다.
- Red-Black Tree는 각 노드를 1개의 비트만으로 표현한다.
- AVL Tree는 2개의 비트로 표현한다.
- 매우 큰 크기의 데이터 셋에 대해서 처리한다고 한다면, Red-Black Tree가 메모리 관점에서 더 유리하다.
LinkedList → Tree로 변경하기 : treeifyBin 메소드
/**
* Replaces all linked nodes in bin at index for given hash unless
* table is too small, in which case resizes instead.
*/
final void treeifyBin(Node<K,V>[] tab, int hash) {
int n, index; Node<K,V> e;
if (tab == null || (n = tab.length) <MIN_TREEIFY_CAPACITY) // 1
resize();
else if ((e = tab[index = (n - 1) & hash]) != null) { // 2
TreeNode<K,V> hd = null, tl = null; // 3
do { // 4
TreeNode<K,V> p = replacementTreeNode(e, null); // 5
if (tl == null) // 6(if-else문)
hd = p;
else {
p.prev = tl;
tl.next = p;
}
tl = p;
} while ((e = e.next) != null);
if ((tab[index] = hd) != null) // 7
hd.treeify(tab);
}
}treeifyBin 메소드는 충돌 횟수가 TREEIFY_THRESHOLD 상수 값을 초과하면 실행된다.
treeifyBin 메소드는 주어진 해시에 대한 Node가 LinkedList 구조로 구성되어 있는데 이것이 너무 많이 충돌이 일어나면 O(n)으로 탐색해야하므로, 이 해시에 대한 Node들을 tree 구조로 구성되게 변경한다. 그럼으로써 O(logN)으로 탐색할 수 있다.
- treeifyBin 메소드는 먼저, 이 map이 (table이) 일부 해시에 대한 값 linkedlist가 tree화 될 만큼 배열의 크기가 큰지 검증한다.
- 해시 충돌이 일어나는 이유는 해시값을 산정하는 알고리즘이 적절하지 않게 정의됨과 더불어, 배열의 크기가 너무 작아서 일어날 수 있다.
- 왜냐하면 인덱스의 값은
해시값 % 크기로 산정되기 때문이다. - 따라서, 트리로 만들만큼 배열의 크기가 큰지 검증하는
MIN_TREEIFY_CAPACITY상수를 통해 이를 검증한다.MIN_TREEIFY_CAPACITY의 값은 64다. - 만약 배열의 크기가 작아서 이 검증에 실패한다면,
resize()메소드를 통해 배열의 크기를 늘린다.
- 배열의 크기가 충분하다면, 주어진 해시에 대한 LinkedList 중 첫번째 Node(변수 e)가 null인지 확인한다.
- null이면 작업을 중단한다.
- LinkedList를 사용할때에는 Node를 사용했지만, Tree를 사용할때는 TreeNode를 사용한다.
TreeNode클래스는LinkedHashMap.Entry클래스의 자식 클래스다.- LinkedHashMap은 HashMap의 자식 클래스다.
LinkedHashMap.Entry클래스는HashMap.Node클래스의 자식 클래스다.- 따라서,
TreeNode클래스는HashMap.Node클래스의 자식 클래스다.
- 이 해시에 대한 LinkedList에 속한 Node<K,V> 모두를 while문을 통해 하나씩 TreeNode로 바꾼다.
- 이 Node를 TreeNode로 생성할 때에는
replacementTreeNode메서드를 이용한다. - TreeNode도 LinkedList일때 사용한 Node 처럼 next 필드를 사용하고, 추가로 prev 필드를 통해서 이 TreeNode 전후의 TreeNode를 설정한다.
- TreeNode를 모두 생성하고, 모두 연결했으므로 이를 하나의 Tree 형태로 만들기 위해서 첫번째 TreeNode를 가지고 tree를 생성한다.
최종적으로 tree를 생성할 때는, TreeNode의 treeify 메소드를 사용한다. (위 7번 과정)
final void treeify(Node<K,V>[] tab) {
TreeNode<K,V> root = null;
for (TreeNode<K,V> x = this, next; x != null; x = next) { // 1
next = (TreeNode<K,V>)x.next;
x.left = x.right = null;
if (root == null) { // 2
x.parent = null;
x.red = false;
root = x;
}
else {
K k = x.key;
int h = x.hash;
Class<?> kc = null;
for (TreeNode<K,V> p = root;;) { // 3
int dir, ph;
K pk = p.key;
if ((ph = p.hash) > h)
dir = -1;
else if (ph < h)
dir = 1;
else if ((kc == null &&
(kc =comparableClassFor(k)) == null) ||
(dir =compareComparables(kc, k, pk)) == 0)
dir =tieBreakOrder(k, pk); // 4
TreeNode<K,V> xp = p;
if ((p = (dir <= 0) ? p.left : p.right) == null) {
x.parent = xp;
if (dir <= 0)
xp.left = x;
else
xp.right = x;
root =balanceInsertion(root, x);
break;
}
}
}
}
moveRootToFront(tab, root);
}TreeNode에 연결된 모든Node를 탐색하면서 Tree로 만든다.- 처음 탐색하는 TreeNode는 this인데, 위
treeifyBin메소드에서 첫번째TreeNode를 통해 이treeify메소드를 호출했으므로 처음 탐색하는TreeNode는 첫번째TreeNode이다.
- 처음 탐색하는 TreeNode는 this인데, 위
- 첫번째
TreeNode는 rootTreeNode가 된다. - 루트
TreeNode부터 순회하면서TreeNode간의 순서를 지정한다. - 트리 구성시, hashcode 의 값이 같으면서 오브젝트가 동일하지 않은 경우 트리의 ordering 을 위해
tieBreakOrder메소드를 사용한다.- 트리 순회 시 사용하는 대소 판단 기준은 해시 함수 값이다.
- TreeNode에서 어떤 두 키의comparator 값이 같다면 서로 동등하게 취급된다.
- 그런데 어떤 두 개의 키의 hash 값이 서로 같아도 이 둘은 서로 동등하지 않을 수 있다.
- 따라서 어떤 두 개의 키에 대한 해시 함수 값이 같을 경우, 임의로 대소 관계를 지정할 필요가 있는 경우가 있다.
- 해시 값을 대소 판단 기준으로 사용하면 Total Ordering에 문제가 생기므로, 이를 조율하는 메서드가
tieBreakOrder메소드다.
Red-Black Tree
규칙
- 모든 노드는 빨강색 혹은 검정색이다.
- Root 노드는 검정색이다.
- 새롭게 노드를 추가할 때에는, 빨강색 노드로 추가한다.
- Root 노드 부터 Leaf 노드까지의 모든 경로는 같은 개수의 검정색 노드를 가지고 있어야한다.
- 어떠한 경로도, 연속으로 빨강색 노드를 가질 수 없다.
- Null인 경우는 검정색 노드로 생각할 수 있다.
Rebalance ( 트리를 균형있게 만드는 방법 )
- Rotate : Black Aunt를 가질 경우
- Rotation 후에는, 부모 노드는 검정색, 자식 노드는 빨강색 노드의 구조이다.
- Color Flip : Red Aunt를 가질 경우
- Color Flip 후에는, 부모 노드는 빨강색, 자식 노드는 검정색 노드의 구조이다.
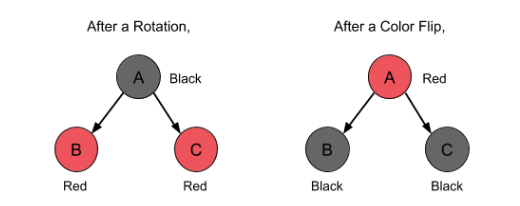
Red-Black Tree Rebalance 예제
파랑색을 검정색 노드로, 핑크색을 빨강색 노드로 생각한다.
1번 예제
- 올바른 균형의 Red-Black Tree에 7을 추가한다.
- 5 노드와 7 노드에 연속적인 빨강색 노드가 있는 문제가 발생했다. 이때, Aunt 노드인 1번 노드가 빨강색이기 때문에, Color Flip 방법을 사용한다.
- 1, 5번 노드는 Flip되어 검정색 노드로 색깔을 변경했다. 3번 노드는 Flip되어야하나, 루트 노드이므로 검정색 노드로 유지한다.

2번 예제
- 올바른 균형의 Red-Black Tree에 6을 추가한다.
- 7 노드와 6 노드에 연속적으로 빨강색 노드가 있는 문제가 발생했다. 이때, Aunt 노드는 없기 때문에(null) 검정색 노드라고 생각한다. Black Aunt의 상황에는 Rotate 방법을 사용한다.
- 5, 7, 6 노드를 Rotate 하여 6을 부모 노드로, 5와 7을 자식 노드로 가진다.
- Rotate 방법을 적용한 이후에는 부모 노드는 검정색 노드, 자식 노드를 빨강색 노드를 가져야하므로 6 노드와 5 노드의 색깔을 변경한다.

3번 예제
- 올바른 균형의 Red-Black Tree에 8을 추가한다.
- 7 노드와 8 노드가 연속적으로 빨강색 노드를 가져 Rebalancing 해야한다. 이때, Aunt Node인 5 노드가 빨강색 노드이므로, Color Flip 방법을 사용한다.
- 6 노드는 빨강색 노드로, 5, 7 노드는 검정색으로 변경하여, 트리가 올바르게 Rebalancing 되었다. 이 트리에 9를 추가한다.
- 8 노드와 9 노드가 연속적으로 빨강색 노드를 가져 Rebalancing 해야한다. 이때, Aunt Node가 null이므로 검정색 노드라고 생각하므로, Rotate 방법을 사용한다.
- 7, 8, 9 노드에 대해 Rotate를 적용하여 8을 부모 노드로, 7, 9 를 자식 노드로 갖는다. 올바른 트리로 Rebalancing 되었다.
이 때, 루트 - 리프 노드의 각 경로를 살펴 보면 모두 2개씩 검정색 노드를 가지는, 올바른 Red-Black Tree임을 알 수 있다.

AVL Tree와의 차이점
AVL Tree의 규칙
- 왼쪽 Sub Tree와 오른쪽 Sub Tree간 높이의 차이는 0 또는 1 이어야한다.
- 1번 조건을 위반할 경우( 높이 차이가 2이상일 경우 ), Rebalancing 한다.
Red-Black Tree VS AVL Tree
| 비교 대상 | Red Black Tree | AVL Tree |
|---|---|---|
| 조회(탐색) | 엄격히 균형 잡힌 것은 아니기 때문에, 비교적 탐색이 빠르지 않다. | 엄격히 균형잡힌 트리이기 때문에, 빠르게 조회할 수 있다. |
| 색깔 | 빨강색과 검정색 노드로 이루어져있다. | 해당 없음 |
| 삽입, 삭제 | Red Black Tree는 AVL Tree에 비해 균형이 엄격하지 않아 rotation 작업이 적기 때문에, 더 빨리 삽입과 삭제를 수행한다. | AVL tree는 엄격히 균형잡힌 트리이므로, 삽입과 삭제가 복잡하다. |
| 저장 용량 | 노드당 1비트 | 각 노드의 balance factor 또는 높이를 저장하므로, 노드당 정수값을 저장한다. |
| 사용 | map, multimap, multiset등 | 빠른 탐색을 요하는 DB |
| Balance Factor | 해당 없음 | 각 노드는 1, 0, -1 값 중 하나를 가지는 balance factor를 가지고 있다. |
| Balancing | balancing을 위한 처리량이 적다. Rotation도 왼쪽, 오른쪽으로 최대 두가지 뿐이다. | Left Left, Right Right, Left Right, Right Left의 Rotation을 할 수 있어, balancing을 위해 비교적 처리량이 많다. |
레퍼런스
Figure 2. Example of Separate Chaining Method
Red Black Tree vs AVL Tree - GeeksforGeeks
[자료구조] HashMap 파헤치기 1 (Linked List + Red Black Tree)
'CS' 카테고리의 다른 글
| BASE 속성, CAP 이론 그리고 PACELC 이론 (0) | 2023.09.05 |
|---|---|
| 가상 메모리 (0) | 2023.08.22 |